Regression Using History Relevance: Intro to Partial Sample Regression
by Hansen Pei
Join the Reading Group and Community: Stay up to date with the latest developments in Financial Machine Learning!
LEARN MORE ABOUT PAIRS TRADING STRATEGIES WITH “THE DEFINITIVE GUIDE TO PAIRS TRADING”
Introduction
Ordinary least squares (OLS) regression is probably the most commonly used statistical method in quantitative finance (and likely in other quantitative fields). It is very fast to compute, and the results are often quite interpretable. Due to its simplicity, it serves as the cornerstone for many more complex statistical or machine learning models. Also, it has been studied so thoroughly historically, that many of its limitations can be covered by various techniques. For example, the original OLS model treats all instances in the training set of equal importance, and one of the common approaches is to introduce weights on the instances to reflect our beliefs.
In this article, we aim to introduce a systematic and elegant approach to incorporate history’s relevance to the regression process.
Briefly speaking, this method ranks all history instances based on their “relation” to the current input independent variables and selects those that are more informative and similar to regress on.
Also, we present the proof that its limit case indeed coincides with the OLS, providing another insight to interpret the OLS model.
The history-weighted regression model (sometimes called partial sample regression) is developed by Megan Czasonis, Mark Kritzman, and David Turkington in three papers (links at the end of the post). We use the consensus in [Relevance] for notation consistency. This regression method is currently available in the MLFinlab as mlfinlab.regression.history_weight_regression.
Definitions and Concepts
Intuitively, when we look at historical data to make a reasonable guess of the current situation, we tend to at first identify similar cases to our current situation. For example, say we are trying to gauge a stock’s price with some companies’ fundamental data (could be more than 1 company), we would like to look at situations similar to the current environment. Then amongst those similar cases, we tend to take a deeper look at those that are farther away from the historical mean, because they usually bear more interesting information, and the average cases are more inclined to be influenced by just noise.
We will introduce a few key concepts in this section, and to keep the notations consistent in this article, we assume all vectors are column vectors (the common way in linear algebra textbooks, though not in some machine learning books), and an N-by-k matrix storing data has n instances and k features (The usual way people implement in pandas.).
Mahalanobis Distances
Suppose we have an N-by-k data matrix ![]() , with
, with ![]() -many instances and
-many instances and ![]() -many features. Think about
-many features. Think about ![]() as our training set. Then we can calculate the features’ covariance matrix (k-by-k) as
as our training set. Then we can calculate the features’ covariance matrix (k-by-k) as
![]()
Assuming the ![]() is symmetric positive definite (i.e., features are independent and there are no 0 variances within themselves), then we can calculate the Fisher information matrix
is symmetric positive definite (i.e., features are independent and there are no 0 variances within themselves), then we can calculate the Fisher information matrix ![]() (though strictly speaking it is only true asymptotically in the frequentist sense, but we borrow the name here anyway).
(though strictly speaking it is only true asymptotically in the frequentist sense, but we borrow the name here anyway).
The Mahalanobis Distance of two instances ![]() are defined as follows in the quadratic form:
are defined as follows in the quadratic form:
![]()
This is indeed a valid definition for distance (or norm) because ![]() is also symmetric and positive definite. Intuitively, because
is also symmetric and positive definite. Intuitively, because ![]() records the variances for each feature around the mean among our data,
records the variances for each feature around the mean among our data, ![]() records how tight the training data are for each feature around the mean. Therefore,
records how tight the training data are for each feature around the mean. Therefore, ![]() is the amount of information along the direction
is the amount of information along the direction ![]() : The larger the value, the larger the amount of information the direction
: The larger the value, the larger the amount of information the direction ![]() contains.
contains.
Hence ![]() quantifies the amount of information given the training data between two specific instances
quantifies the amount of information given the training data between two specific instances ![]() , and the two instances are arbitrary as they do not have to all come from the training set or test set. We often assume
, and the two instances are arbitrary as they do not have to all come from the training set or test set. We often assume ![]() to be a training instance and
to be a training instance and ![]() to be a test instance for interpretability.
to be a test instance for interpretability.
Similarity
Now we define the similarity between two instances ![]() as the negative of their Mahalanobis distance:
as the negative of their Mahalanobis distance:
![]()
Trivially, when ![]() , they are the most similar pair and the similarity becomes 0, the largest value it can achieve. This quantity, as its name suggests, measures how similar two instances are, based on our training set. The larger the value, the more similar they are, and as a result the less information one can get.
, they are the most similar pair and the similarity becomes 0, the largest value it can achieve. This quantity, as its name suggests, measures how similar two instances are, based on our training set. The larger the value, the more similar they are, and as a result the less information one can get.
Informativeness
Remember that ![]() is the amount of information along the direction
is the amount of information along the direction ![]() away from the mean, we can therefore define the informativeness as below:
away from the mean, we can therefore define the informativeness as below:
![]()
where ![]() is the mean of our training data
is the mean of our training data ![]() for each feature. The larger the value, the less similar
for each feature. The larger the value, the less similar ![]() is to the mean, and therefore the more information it brings.
is to the mean, and therefore the more information it brings.
Note that similarity and informativeness are addressing two different aspects of the data. They are in some sense the opposite of each other but with some nuances here: similarity is used to measure between two instances whereas informativeness is used to measure between one instance to the training data. We will combine the two together to form the key value for the history weighted regression method, called relevance.
Relevance and Subsample
Now we can define the relevance value between two instances ![]() as follows:
as follows:
(1) 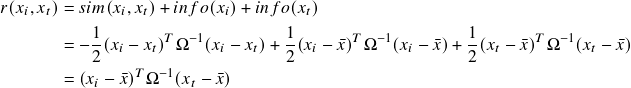
Relevance is interpreted as the sum of similarity and informativeness for ![]() , where
, where ![]() is in the training set, and
is in the training set, and ![]() is a test instance. Intuitively, when the in-sample instance and the test instance pair
is a test instance. Intuitively, when the in-sample instance and the test instance pair ![]() are similar and give great information, their relevance value will be greater.
are similar and give great information, their relevance value will be greater.
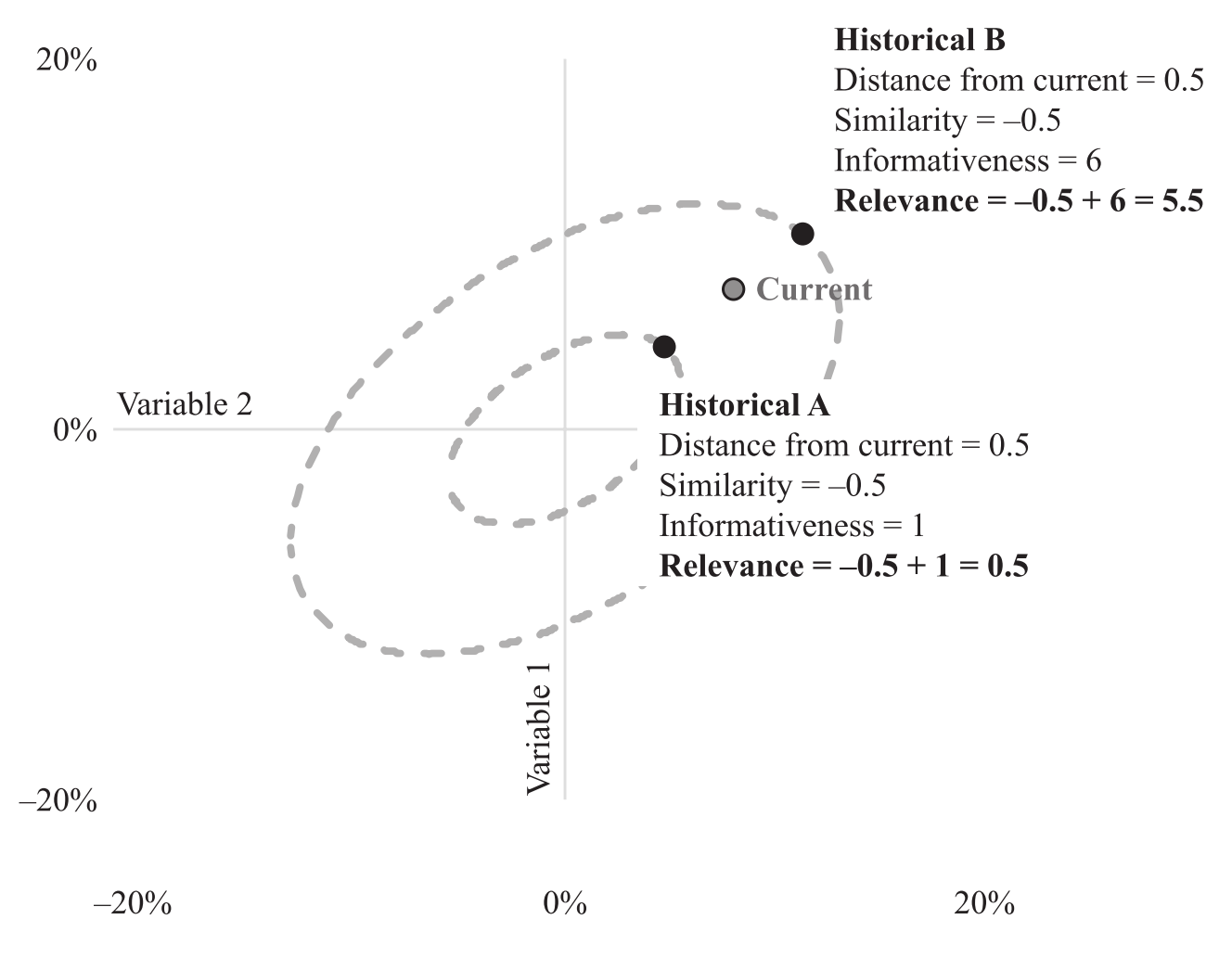
Indeed, relevance is the value to quantify the thought process we had in the beginning for gauging the stock’s price using companies fundamental data. The figure below gives a good visual illustration of relevance. Note that the two historical events are on their elliptical orbits of fixed amounts of informativeness.
Fig. 1: An illustration of the relationship between similarity, informativeness, and relevance.
We choose historical event B to be more relevant to our current case than event A.
(Figure from [Addition by Subtraction])
Conduct Predictions
Now we have an instance in the independent variable ![]() , we aim to make a prediction
, we aim to make a prediction ![]() based on
based on ![]() . Say the training data for the independent variable is in the matrix N-by-K
. Say the training data for the independent variable is in the matrix N-by-K ![]() and the dependent variable is in the N-by-1 vector
and the dependent variable is in the N-by-1 vector ![]() (1 instance, N features).
(1 instance, N features).
Workflow
- Calculate all relevance between
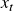 and each row of
and each row of 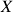 :
: 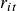 where
where 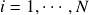 .
. - Rank all the instances in relevance and pick the instances in top
![Rendered by QuickLaTeX.com q \in (0, 1]](https://hudsonthames.org/wp-content/ql-cache/quicklatex.com-1074247cc99f2e7221b15e033b84bf50_l3.png) quantiles to form a subsample with
quantiles to form a subsample with  instances.
instances. - Conduct a prediction using the formula
![]()
where ![]() is the subsample average of the dependent variable in the training set.
is the subsample average of the dependent variable in the training set.
We can read the formula above in two terms: For the first term ![]() , when no information is given about
, when no information is given about ![]() (i.e.,
(i.e., ![]() ), the best prediction we can formulate for the unknown
), the best prediction we can formulate for the unknown ![]() is
is ![]() . The second term can be interpreted as a weighted average by the relevance of historical deviations for the dependent variable, and the weights are computed by
. The second term can be interpreted as a weighted average by the relevance of historical deviations for the dependent variable, and the weights are computed by ![]() .
.
Tip
It is a good practice to rescale ![]() for each feature, for example, by the number of standard deviations from its mean. This will in general produce a covariance matrix with much smaller condition numbers, and thus for the Fisher information matrix since their condition numbers are equal. A smaller condition number is more stable numerically in the calculation, especially when we initially calculate the inverse of the covariance matrix. Because every step in the workflow is linear, the final prediction will not change and does not need to be re-scaled.
for each feature, for example, by the number of standard deviations from its mean. This will in general produce a covariance matrix with much smaller condition numbers, and thus for the Fisher information matrix since their condition numbers are equal. A smaller condition number is more stable numerically in the calculation, especially when we initially calculate the inverse of the covariance matrix. Because every step in the workflow is linear, the final prediction will not change and does not need to be re-scaled.
Connection with OLS
We aim to show that, when we do not reduce to a subsample (i.e., ![]() or equivalently
or equivalently ![]() ), then the above prediction coincides with the prediction given by OLS. First, without loss of generality assume
), then the above prediction coincides with the prediction given by OLS. First, without loss of generality assume ![]() and
and ![]() have means of 0. Then plug
have means of 0. Then plug
![]()
into the prediction formula, we get
(2) 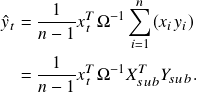
Where ![]() and
and ![]() are the associated subsamples selected by relevance with
are the associated subsamples selected by relevance with ![]() . Since we assume
. Since we assume ![]() , equivalently
, equivalently ![]() , we have
, we have
(3) 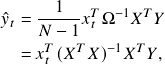
which is indeed the formula for OLS.
Summary and Comments
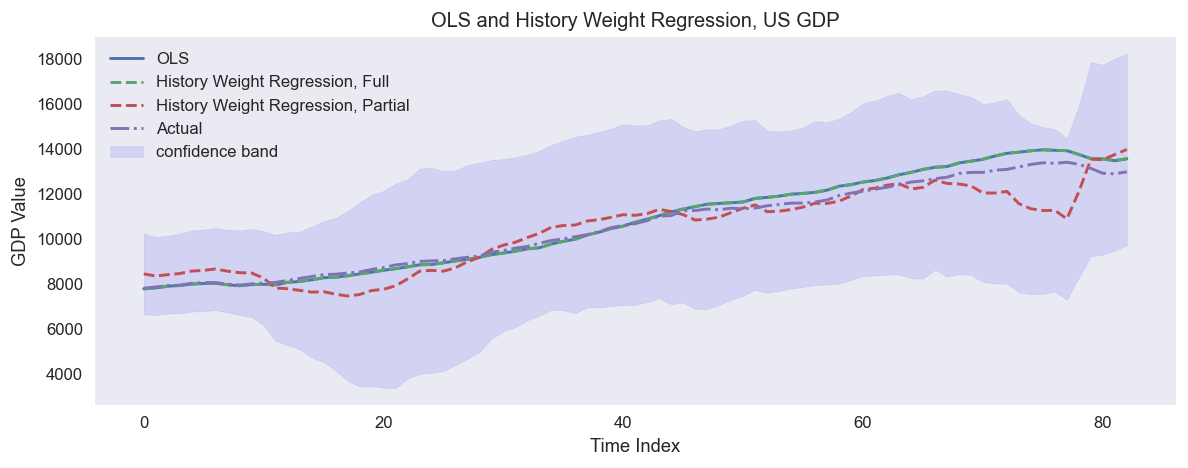
Fig. 2: An example of predicting US quarterly GDP in 1988-2009 using quarterly fundamental data from 1959-1987: real personal consumption expenditures, real federal consumption expenditures & gross investment, unemployment rate, and M1 (seasonally adjusted). The full sample regression collides with OLS.
- The prediction from a linear regression equation is mathematically equivalent to a weighted average of all past values of the dependent variable in which the weights are the relevance of the independent variables.
- This equivalence allows one to form a relevance-weighted prediction of the dependent variable by using only a subsample of relevant observations. This approach is called partial sample regression.
- Like partial sample regression, an event study can separate relevant observations from non-relevant observations, but it does so by identification rather than systematically and mathematically.
- We should also note that this approach is different from the traditionally defined weighted least squares regression, which uses fixed weights regardless of the data point being predicted and applies the weights to calculate the covariance matrix among predictors.
- This regression method is different from performing separate regressions on subsamples of the most relevant observations; In a separate regression approach, the covariance matrix used for estimation would also be based on the subsample, whereas we always use the full-sample covariance matrix.
- The calculation is invariant under linear re-scale of
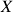 . Rescale to get a better condition number for
. Rescale to get a better condition number for 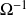 .
. - This method is conceptually different from PCA, where feature importance is instead considered. This regression method considers importance in instances, not features. However, one can combine the PCA transformation and the partial sample regression, and if all principal components are considered, the prediction result will be identical compared to directly working with
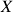 .
.
References
All the following works are done by Megan Czasonis, Mark Kritzman and David Turkington.