Pairs Trading with Markov Regime-Switching Model

by Andy Lin and Illya Barziy

Join the Reading Group and Community: Stay up to date with the latest developments in Financial Machine Learning!

LEARN MORE ABOUT PAIRS TRADING STRATEGIES WITH “THE DEFINITIVE GUIDE TO PAIRS TRADING”

Introduction

Traditional pairs trading strategies are prone to failures when fundamental or economic reasons cause a structural break and the pair of assets that were expected to move together are no longer having a strong relationship. Such a break may result in asset price spread having abnormally high deviations failing to revert to its historical mean values. Under these circumstances, betting on the spread to revert to its historical mean would result in a loss. To overcome the problem of detecting whether the deviations are temporary or longer-lasting, Bock, M. and Mestel, R. (2009) bridge the literature on Markov regime-switching models and the scientific work on statistical arbitrage to develop a set of useful trading rules for pairs trading.

Below we will first cover the assumptions behind the approach proposed in the original paper, then introduce the strategy proposed by the authors, and finally, the way to execute the strategy step by step.

This is the second article in a series dedicated to Time Series Approach Pairs Trading Strategies. If you’ve missed previous ones, we are attaching links to them below:

Optimal Trading Thresholds for the O-U Process

Assumptions

Series Formed by the Trading Pair

The model defines the price series $X_t$ formed by the trading pair as,

$X_t = \mu_{s_t} + \epsilon_t$

where $E[\epsilon_t] = 0$ , $\sigma^2_{\epsilon_t} = \sigma^2_{s_t}$ and $s_t$ denotes the current regime determined by the Markov regime-switching model.

Markov Regime-Switching Model

A two-state, first-order Markov-switching process for $s_t$ is considered with the following transition probabilities:

$\Bigg\{ \begin{matrix} prob[s_t = 1 | s_{t-1} = 1] = p \\ prob[s_t = 2 | s_{t-1} = 2] = q \\ \end{matrix}$

where $1$ indicates a regime with a higher mean ( $\mu_{1}$ ) while $2$ indicates a regime with a lower mean ( $\mu_{2}$ ).

Strategy

The idea behind the Markov regime-switching model strategy is straightforward. Suppose the spread process is in the high regime, and we observe that it deviated below the mean by a certain amount. In that case, we take a long trade on the spread only if the probability of the process staying in the high regime is bigger than a certain threshold. In the low regime, the logic is exactly the opposite.

The trading signal $z_t$ is determined in the following way:

$Case\ 1 \ \ current\ regime = 1$

$z_t = \left\{\begin{array}{l} +1,\ if\ X_t \leq \mu_1 - \delta \cdot \sigma_1 \wedge P(s_t = 1 | X_t) \geq \rho \\ -1,\ if\ X_t \geq \mu_1 + \delta \cdot \sigma_1 \\ 0,\ otherwise \end{array}\right.$

$Case\ 2 \ \ current\ regime = 2$

$z_t = \left\{\begin{array}{l} +1,\ if\ X_t \leq \mu_2 - \delta \cdot \sigma_2 \\ -1,\ if\ X_t \geq \mu_2 + \delta \cdot \sigma_2 \wedge P(s_t = 2 | X_t) \geq \rho\\ 0,\ otherwise \end{array}\right.$

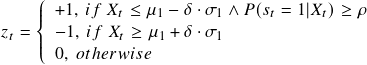
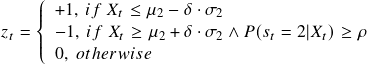
where $P(\cdot)$ denotes the smoothed probabilities for each state, $\delta$ and $\rho$ denote the standard deviation sensitivity parameter and the probability threshold of the trading strategy, respectively.

To be more specific, the trading signal can be described as,

$Case\ 1 \ \ current\ regime = 1$

$\left\{\begin{array}{l} Open\ a\ long\ trade,\ if\ X_t \leq \mu_1 - \delta \cdot \sigma_1 \wedge P(s_t = 1 | X_t) \geq \rho \\ Close\ a\ long\ trade,\ if\ X_t \geq \mu_1 + \delta \cdot \sigma_1 \\ Open\ a\ short\ trade,\ if\ X_t \geq \mu_1 + \delta \cdot \sigma_1 \\ Close\ a\ short\ trade,\ if\ X_t \leq \mu_1 - \delta \cdot \sigma_1 \wedge P(s_t = 1 | X_t) \geq \rho \\ Do\ nothing,\ otherwise \end{array}\right.$

$Case\ 2 \ \ current\ regime = 2$

$\left\{\begin{array}{l} Open\ a\ long\ trade,\ if\ X_t \leq \mu_2 - \delta \cdot \sigma_2 \\ Close\ a\ long\ trade,\ if\ X_t \geq \mu_2 + \delta \cdot \sigma_2 \wedge P(s_t = 2 | X_t) \geq \rho\\ Open\ a\ short\ trade,\ if\ X_t \geq \mu_2 + \delta \cdot \sigma_2 \wedge P(s_t = 2 | X_t) \geq \rho\\ Close\ a\ short\ trade,\ if\ X_t \leq \mu_2 - \delta \cdot \sigma_2 \\ Do\ nothing,\ otherwise \end{array}\right.$

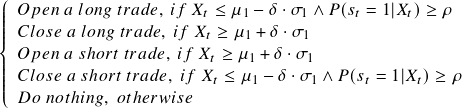
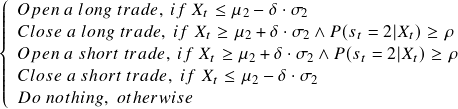
Steps to Execute the Strategy

Step 1: Select a Trading Pair

In the original paper, the authors used the DJ STOXX 600 component as the asset pool and applied the cointegration test to perform pairs selection, meaning that if the prices of assets in a pair are cointegrated, they are picked as good candidates to be used in the strategy. One can use the same method as proposed in the original paper or utilize one of the alternative pairs selection methods described in our previous articles:

Step 2: Construct the Spread Series

In their work, authors use $\frac{P^A_t}{P^B_t}$ as the spread series. One can use the same method as in the paper, or other ways of constructing the spread series, like $(P^A_t/P^A_0) - \beta \cdot (P^B_t/P^B_0)$ or $ln(P^A_t/P^A_0) - \beta \cdot ln(P^B_t/P^B_0)$ .

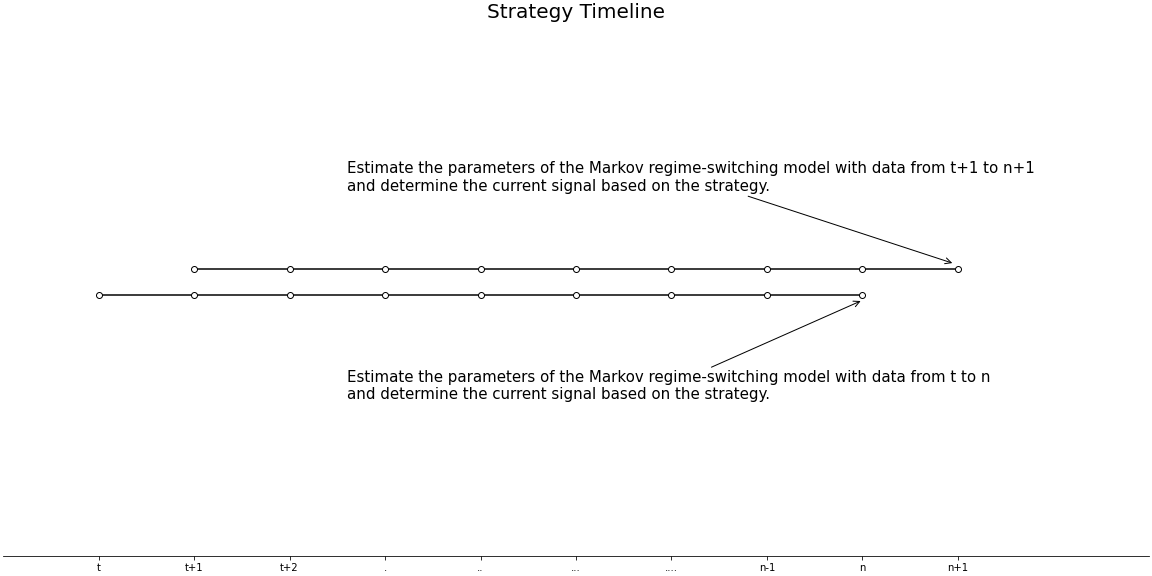
Step 3: Estimate the Parameters of the Markov Regime-Switching Model

Fit the Markov regime-switching model to the spread series with a rolling time window to estimate $\mu_1$ , $\mu_2$ , $\sigma_1$ , $\sigma_2$ and the current regime.

Step 4: Determine the Signal of the Strategy

Determine the current signal based on the strategy and estimated parameters.

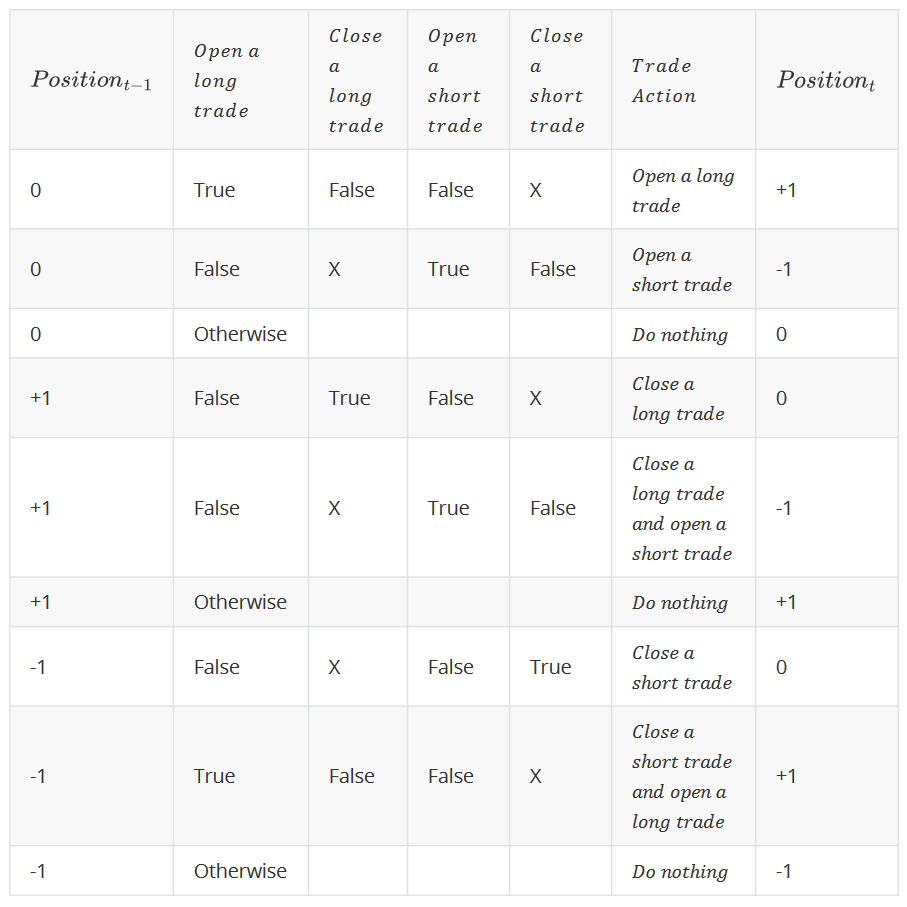
Step 5: Decide the Trade

Decide the trade based on the signal at time $t$ and the position at time $t - 1$ . Possible combinations are listed below:

where X denotes the don’t-care term, the value of X could be either True or False.

Conclusion

The paper provides a pairs trading strategy based on the Markov regime-switching model, which is innovative and varies from traditional models used for pairs trading. It also provides a method to detect structural breaks of the spread formed by the pair of assets so that it’s possible to reduce the chance of encountering a loss due to structural changes.

It is worth noting that this strategy will fail if there is a regime higher than the current high regime or a regime lower than the current low regime in the future. At this time, since no such regime has appeared in the historical data, the strategy can’t detect the structural break successfully. To overcome this problem, we can simply change the signal as follows:

$Case\ 1 \ \ current\ regime = 1$

$\left\{\begin{array}{l}Open\ a\ long\ trade,\ if\ X_t \leq \mu_1 - \delta \cdot \sigma_1 \wedge P(s_t = 1 | X_t) \geq \rho \\Close\ a\ long\ trade,\ if\ X_t \geq \mu_1 + \delta \cdot \sigma_1 \\ Close\ a\ short\ trade,\ if\ X_t \leq \mu_1 - \delta \cdot \sigma_1 \wedge P(s_t = 1 | X_t) \geq \rho \\ Do\ nothing,\ otherwise\end{array}\right.$

$Case\ 2 \ \ current\ regime = 2$

$\left\{\begin{array}{l} Close\ a\ long\ trade,\ if\ X_t \geq \mu_2 + \delta \cdot \sigma_2 \wedge P(s_t = 2 | X_t) \geq \rho\\ Open\ a\ short\ trade,\ if\ X_t \geq \mu_2 + \delta \cdot \sigma_2 \wedge P(s_t = 2 | X_t) \geq \rho\\ Close\ a\ short\ trade,\ if\ X_t \leq \mu_2 - \delta \cdot \sigma_2 \\Do\ nothing,\ otherwise\end{array}\right.$

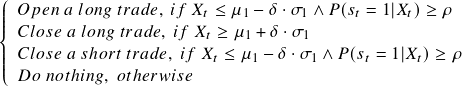
So we only make the long trade at the high regime and only make the short trade at the low regime. This can decrease the risk of enormous losses when the regimes that don’t appear in historical data are encountered.

Another thing that needs to be noted is that the Markov regime-switching model often fails to fit when a switching mean of the process and switching variance of the process are assumed. This will make the signal impossible to determine, which in turn makes the strategy impossible to execute.