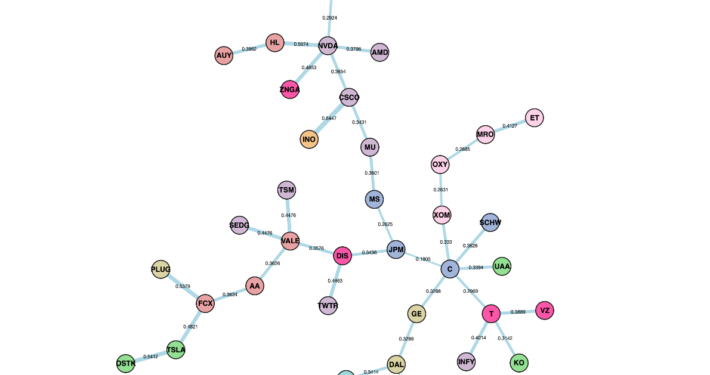
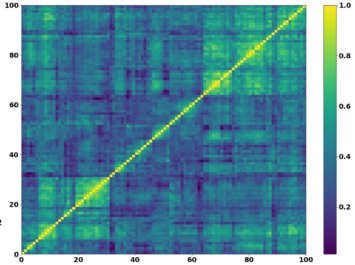
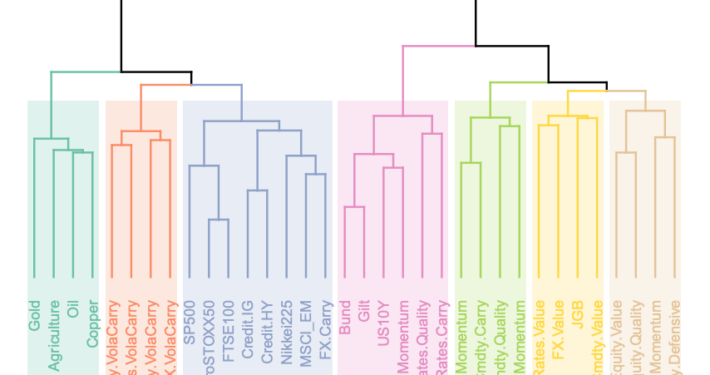
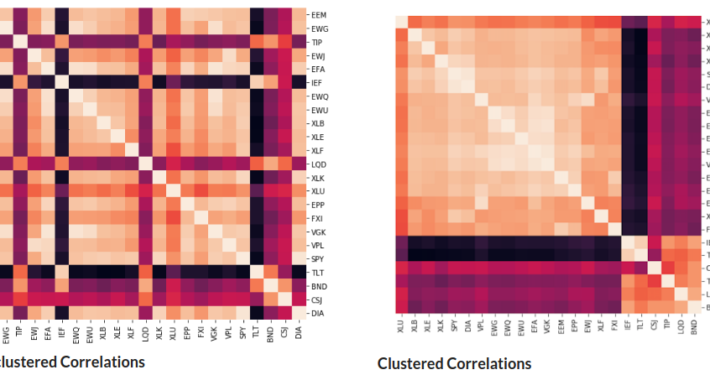
Pairs selection is the first crucial step to building a pairs trading strategy. And it is no surprise, to perform it correctly, one must diligently examine, compare and contrast numerous test results, graphs and characteristics. For example, cointegration analysis alone can be performed in one of two methods – utilizing the Engle-Granger approach or the Johansen approach. To truly have the complete picture of the pairs suitability, with the Engle-Granger approach, the researcher should perform the test(and further analysis) for both possible combinations, A/B or B/A, in a pair since it is sensitive to which asset we choose to be the “dependent” one.
The Johansen test, in turn, provides multiple cointegration vectors, which also should be examined separately and taken into account. Not to mention the possible analysis of the residuals, auto-correlation tests, etc., brings even more data to the table for you to make your judgement.
And now, we have two options: memorize everything or constantly switch between numerous parameters and plots to check, contrast and compare. It results in loading your brain with tons of ‘noise’ that distracts from focusing on the evaluation itself. But it doesn’t have to be this way. Data analysis thrives when there is order, accessibility and clarity. And what embodies these three qualities better than combining everything into an interactive well-rounded tear sheet?






































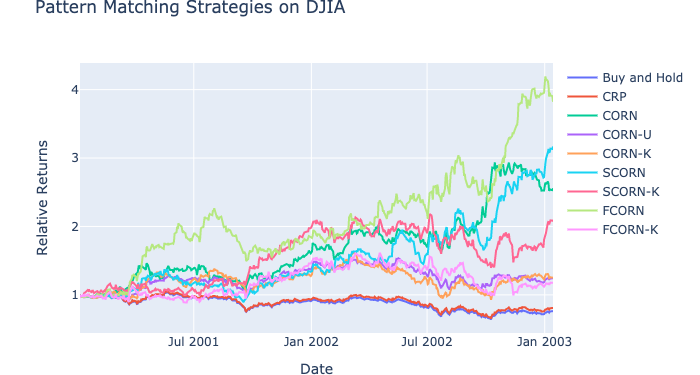
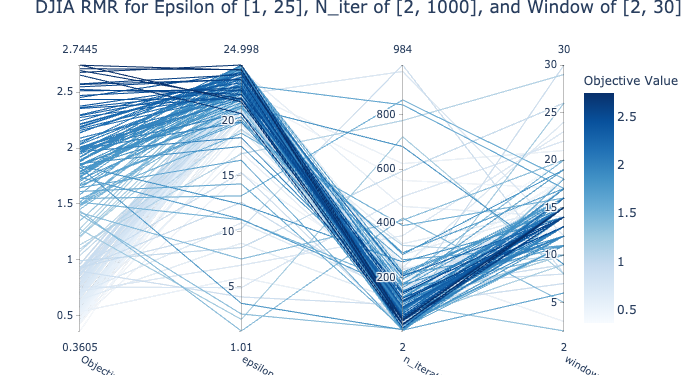
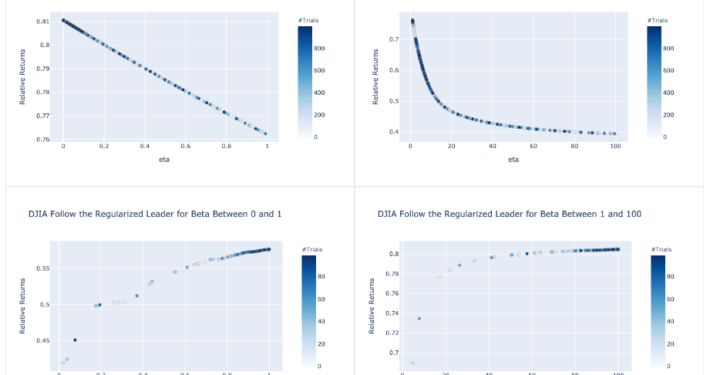



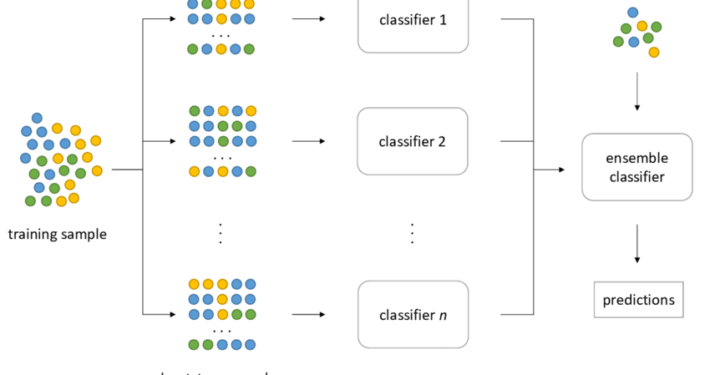 https://www.researchgate.net/figure/The-bagging-approach-Several-classifier-are-trained-on-bootstrap-samples-of-the-training_fig4_322179244
https://www.researchgate.net/figure/The-bagging-approach-Several-classifier-are-trained-on-bootstrap-samples-of-the-training_fig4_322179244




































































 https://www.researchgate.net/figure/The-bagging-approach-Several-classifier-are-trained-on-bootstrap-samples-of-the-training_fig4_322179244
https://www.researchgate.net/figure/The-bagging-approach-Several-classifier-are-trained-on-bootstrap-samples-of-the-training_fig4_322179244








Dynamically combining mean reversion and momentum investment strategies
Statistical ArbitrageBy Ruth du Toit
Exploring Mean Reversion and Momentum Strategies in Arbitrage Trading
Our recent reading group examined mean reversion and momentum strategies, drawing insights from the article, “Dynamically combining mean reversion and momentum investment strategies” by James Velissaris. The aim of the paper was to create a diversified arbitrage approach that combines mean reversion and momentum strategies to exploit the strengths of both strategies.
Mean reversion and momentum strategies have distinct characteristics. Mean reversion strategies centre around stocks reverting to their mean values and capitalising on relative mispricing among stocks. In contrast, momentum strategies focus on stocks that have shown strong recent performance and are expected to continue that trend.
Set-Up
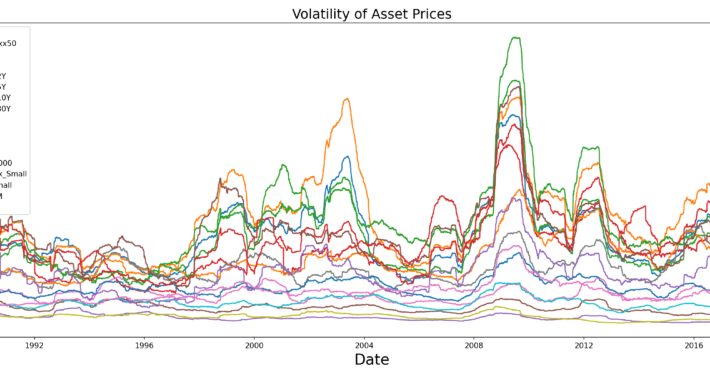
The dataset for the study is made up of an in-sample period from November 1, 2005, to October 31, 2007 which includes the Quant Quake of August 2007, and an out-of-sample period from November 1, 2007, to October 30, 2009 which includes the Global Financial Crisis of 2008. For the mean reversion model, daily closing price data from the S&P 500 index were utilised whereas the momentum strategy incorporated daily closing price data sourced from Bloomberg for ten different stock market indices.
Inspired by Avellaneda and Lee’s work on ‘Statistical Arbitrage in the U.S. Equities Markets’, the equity mean reversion model aimed to maintain a market-neutral position. However, its failure to meet this primary objective casts doubt on the model’s overall effectiveness. Furthermore, Quadratic programming was employed for portfolio rebalancing, focusing on optimising asset allocation.
In-Sample Performance
In the article, the mean reversion strategies proved to be highly effective within the in-sample environment (although this shouldn’t be surprising).
The problem with in-sample results
Mean reversion’s apparent effectiveness at the in-sample dataset is based on the use of historical market knowledge and parameter optimisation to align with past data. However, it’s important to be sceptical of in-sample data, and to approach out-of-sample performance expectations with caution, as historical predictability may not necessarily translate to future periods.
In the reading group, we discussed possible ways to improve the generalization of our mean reversion strategies to the out-of-sample dataset. Can techniques such as regularisation or cross-validation offer a solution?
Addressing these challenges is important to ensure the robustness of trading strategies when they are used in real-world scenarios. While in-sample performance provides some value, it’s the out-of-sample testing that validates the strategy’s adaptability to changing market conditions. Ultimately, however, what really matters is trading the strategy with real money in a live trading environment.
Out-of-Sample Performance
Momentum, as a strategy, relies on recent price trends, which tend, but are not guaranteed, to continue for longer periods in real markets.
Near the end of the 2008 global financial crisis, Momentum strategies seem to have been effective. Note, however, that the fact that this strategy performed well at the end of 2008 suggests that it may have been capitalising on a potential market recovery during that period.
Market Neutral vs. Hedging Opportunities
While the mean reversion model aspired to a market-neutral stance, it consistently fell short of this target in practice. Although we could argue it could act as a hedge during broader market downturns, according to the paper we might be better off remaining sceptical. Thus, it would be premature to regard mean reversion as a foolproof method for reducing overall risk exposure through low-correlation strategies.
Directions in Trading Strategies
In-sample, mean reversion demonstrates its effectiveness, raising important questions about its adaptability in out-of-sample scenarios. Can the tools such as regularisation and cross-validation help address this challenge? Meanwhile, the Momentum strategy excels in the real world, emphasising the importance of adaptability in our trading approach.
This discussion also serves as a reminder that trading isn’t only about beating the market, it’s also about managing risk.
Stay tuned for further analysis and strategic insights as Hudson & Thames continues to navigate the field of quantitative finance.
For more information about our H&T reading group visit: https://hudsonthames.org/reading-group/